Notas de límites

Limites unilaterales. 

 Imagínate que sufres una pesadilla (por tanto estudiar matemática) en la que te encuentras cerca de una puerta. Decides abrirla, así que te acercas. Te das cuenta que estas cada vez más cerca, pero no alcanzas a tocar el picaporte. Corres tratando de llegar, mas, siempre hay espacio entre tu mano y ese picaporte, no importa cuanto lo intentes.  Esa "pesadilla" tiene nombre matemático "límite".

Desde el punto de vista del conjunto de los números reales, que es denso (infinito e infinitésimo), podemos encontrar entre dos números consecutivos infinitos números:  tomemos dos números, por ejemplo, 4 y 5, busquemos un número real entre ellos, podemos tomar 4,5 que está entre 4 y 5 ® 4 .... 4,5 ..... 5

Ahora busquemos un número entre 4 y 4,5 (podemos tomar 4,3 que está entre 4 y 4,5) ® 4 ...... 4,3 ..... 4,5 

Ahora busquemos un número entre 4 y 4,3 (podemos tomar 4,1 que está entre 4 y 4,3) ® 4 ....... 4,1 ...... 4,3

Ahora busquemos un número entre 4 y 4,1 (podemos tomar 4,08 que está entre 4 y 4,1) ® 4 ...... 4,08 .... 4,1

Ahora busquemos un número entre 4 y 4,08 (podemos tomar 4,001 que está entre 4 y 4,08) ® 4 ..... 4,001 .... 4,08

Podemos seguir así eternamente. Siempre nos podremos acercar al número "4" todo lo que queramos sin llegar a él. Justamente "4" es el límite que no podemos tocar. Como nos acercamos desde valores mayores a 4, se dice que nos "acercamos por la derecha". 

Si nos acercáramos con valores más pequeños, nos "acercaríamos por la izquierda". 

El concepto de límite está íntimamente ligado al concepto de función. Cada uno de los números que se acerca a 4 pueden obtenerse de una ecuación (lineal por ejemplo) como y = 4 + x. Donde al darle valores a xobtenemos "esos" números que se acercan a 4 por derecha e izquierda. Evidentemente, de acuerdo al tipo de ecuación que tengamos, serán los valores de x a tomar en cuenta.

En este caso no nos interesa cuando x = 0, ya que no queremos que "la cuenta" de 4 (que es nuestro límite).

 El valor de x se acerca a "cero" y el valor de "y" (la imagen de la función) se acerca a 4. Para hablar con propiedad, en matemática no se dice "se acerca a" sino "tiende a"; x tiende a cero cuando y tiende a cuatro. Es real, a los que hacemos matemática no nos gusta escribir mucho. Se reemplaza las palabras con símbolos para ahorrar tiempo (el esfuerzo mental se reserva para el problema matemático). Así que en vez de escribir "tiende a" se pone una flecha. De manera que "x tiende a cero" se indica "x ® 0" e "y tiende a cuatro" se escribe como "y ® 4".

Ya estamos un poco más cerca de poder leer "matemáticamente". El límite (lím) suele escribirse indicando debajo de él el valor a que tiende x, seguido de la ecuación que se analiza y (después del igual) se indica el valor del límite.

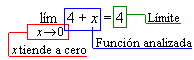
fFuente: https://www.mat.uson.mx/~jldiaz/Limites_laterales-2.htm